Як в евклідової геометрії точка і пряма — головні елементи теорії площин, так і паралелограм є однією з ключових фігур опуклих чотирикутників. З нього, як нитки з клубка, течуть поняття «прямокутника», «квадрата», «ромби» і інших геометричних величин.
Визначення паралелограма
Опуклий чотирикутник, що складається з відрізків, кожна пара з яких паралельна, відомий в геометрії як паралелограм.
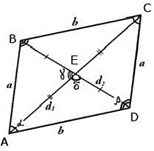
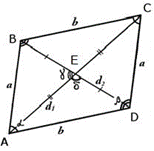
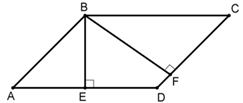
Як виглядає класичний паралелограм зображує чотирикутник ABCD. Сторони називаються підставами (AB, BC, CD і AD), перпендикуляр, проведений з будь-якої вершини на протилежну цій вершині бік, — висотою (BE і BF), лінії AC і BD — діагоналями.
 |
 |
Увага! Квадрат, ромб і прямокутник — це окремі випадки паралелограма.
Сторони і кути: особливості співвідношення
Ключові властивості, за великим рахунком, зумовлені самим позначенням, їх доводить теорему. Ці характеристики наступні:
- Сторони, які є протилежними, — попарно однакові.
- Кути, розташовані протилежно один одному — попарно рівні.
Доказ: розглянемо ∆ABC і ∆ADC, які утворюються внаслідок поділу чотирикутника ABCD прямої AC. ∠BCA=∠CAD і ∠BAC=∠ACD, оскільки AC для них загальна (вертикальні кути для BC||AD і AB||CD, відповідно). З цього випливає: ∆ABC = ∆ADC (друга ознака рівності трикутників).
Відрізки AB і BC у ∆ABC попарно відповідають лініям CD і AD в ∆ADC, що означає їх тотожність: AB = CD, BC = AD. Таким чином, ∠B відповідає ∠D і вони рівні. Оскільки ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, які так само попарно однакові, то ∠A = ∠C. Властивість доведено.