Властивості інтеграла Рімана на відрізку
Для того, щоб безпомилково знаходити площі «кривих» трапецій, розглянемо основні «прийоми», які суттєво полегшать цей процес.
Основні властивості:
Площа трапеції в окремо взятій точці дорівнює нулю. Формулу можна записати так:
![]()
Якщо функція визначена між точками a і b, то справедливо наступне рівність:
![]()
Якщо під інтегральні функції w(x) t(x) визначено на відрізку [k;c] і не мають точок розриву, немає таких точок в яких б функції не мали значення, то справедливо рівність:
![]()
У разі якщо первісна функція визначена (вычислима в кожній точці) і межі інтегрування лежать на відрізку [k;c], тоді під інтегральну функцію можна записати в наступному вигляді:
![]()
Функція j(x) інтегруються на відрізку [a;b], тільки в тому випадку, коли сам відрізок [a;b] належить більшому відрізку [k;c].
Відзначимо, що даний список не включає в себе всі властивості визначеного інтеграла і має продовження. Зазначені «хитрощі» є найбільш поширеними прийомами, однак застосовувати їх потрібно переконавшись в їх «працездатності».
Для більшої наочності знайдемо значення інтеграла, межі інтегрування якого розташовані на відрізку [3;5] для під інтегральної
![]()
Рішення. Згідно з умовою задачі, маємо наступну під певну інтегральну функцію на проміжку
![]()
Можемо отримати наступне:
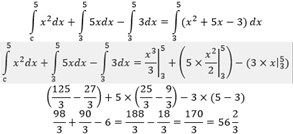
Виходить, що площа криволінійної трапеції буде складати …., цілком очевидно, що можна було і відразу взяти визначений інтеграл від заданої функції не вдаючись до використання властивості, однак такий підхід більш точно розкриває можливості одного з властивостей.
Припустимо, що замість функції за змінною x, перебуває 0 (такий варіант теж вважають функцією і збігається з віссю абсцис). Тоді намагаючись знайти визначений інтеграл від постійної отримаємо:
![]()
Виходить, що якщо під інтегральної функції стоїть нуль, то й первісна, на якому відрізку не була визначена, теж буде дорівнює нулю.
У випадку, якщо потрібно знайти інтеграл від константи, то таке рішення дає приклад вирішення будь-якого многочлена:
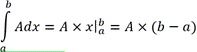
Звідки робимо висновок, що якщо потрібно визначити інтеграл від нуля, то його значення (можна навіть не розписувати) дорівнює нулю, а якщо інтеграл від числа, то різницю між кінцями відрізка потрібно помножити на число під знаком інтеграла.
Важливо! Під час вирішення задач подібного плану, часто доводиться комбінувати зазначені прийоми, для зменшення складності завдання. Але використовуючи такі переходи, не варто забувати, що інтегральна сума завжди повинна збігатися з початковою. Завжди перевіряйте відрізок, на якому збираєтеся інтегрувати, інакше отримане значення буде відрізнятися від дійсного.
