У цій статті розглянуто одну з найбільш важливих теорем стереометрії – теорема про три перпендикулярах. Важливість її полягає в тому, що перш ніж переходити до вирішення складних фігур – сфер, пірамід і паралелепіпедів, необхідно володіти основними законами, що виникають при взаємодіях прямих у просторі.
Базові поняття
Для розуміння суті теореми потрібно володіти базовими поняттями планіметрії.
Часто-густо в геометрії використовується поняття кут. Вимірюються вони в градусах або радіанах. Радіани – незамінна розмірність в тригонометрії, градуси більш звичні нам, тому що прийшли з реального життя.
0 град., 90 град., 180 град. – три типи кутів, які зрозумілі нам не тільки геометричні, але й інтуїтивно. 90 град. (або прямий) – самий, мабуть, популярний тип, тому що активно зустрічається в повсякденному житті.
Перпендикулярностью назвемо таке співвідношення між фігурами (прямими, площинами тощо), при якому кут між ними становить 90 градусів.
Увага! Перпендикуляр – це пряма, яка складає кут 90 град. з іншими прямими або площинами.
Вивчимо термінологію на реальних прикладах:
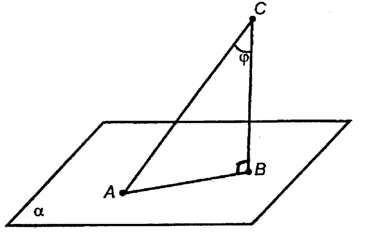
Є площину α. С – точка, яка не лежить на площині. СВ – відрізок, опущеного з точки на площину α і становить з площиною прямий кут. Таким чином СВ ⊥ α. Позначимо похилу, тобто промінь, що виходить теж з С. α перетинає в точці А. АВС – прямокутний трикутник, оскільки СВА дорівнює 90 град.
Теорема
Незважаючи на всю свою простоту, теорема про три перпендикулярах пов’язує між собою кути, знаходяться у різних площинах, тому даний закон вважається досить глобальним в геометрії.

Картина така ж, як у попередньому розділі: є α, точка А, яка лежить за межами α. З цієї точки опущено перпендикуляр, має підставу, також проведений відрізок АС (який є похилою).
Ось як звучить формулювання теореми про три перпендикулярах:
Якщо через основу проведеної похилій проходить пряма і вона утворює кут 90 град. з проекцією, то вона утворює такий же кут з її похилій.
Таким чином, теорема говорить, що, якщо між з і ВС – прямий кут, то він прямій між з і АС.
Доведемо цю теорему:
- ВА – відрізок,що складає з площиною α кут 90 град.;
- СА – відрізок прямої, що є похилій;
- з – проходить через точку С і утворює прямий кут з відрізком ВС.
Проводимо КС || ВА. Значить, він становить кут 90 град. по відношенню до α. Це означає, що він становить кути 90 град. з усіма прямими, що знаходяться в α. Між КС і с — кут 90 градусів, оскільки вона теж належить α.
Будь-які два відрізки, які паралельні один одному, задають площину. Тому існує площину β через відрізки ВА і КС. Пряма з ⊥ СВ і з ⊥ КС, тобто вона становить кут 90 град. з кожної прямої, що належить β, відрізку СА в тому числі.
Нам вдалося довести теорему про три перпендикулярах.
Зворотна теорема про три перпендикулярах
Наведемо точне формулювання зворотної теореми.
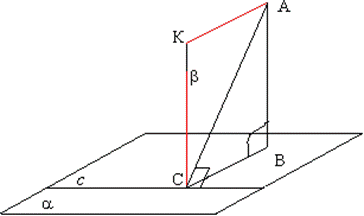
Якщо через основу проведеної похилій проходить пряма і вона становить з похилою кут 90 градусів, то вона утворює такий же кут з її проекцією.
Таким чином, теорема говорить, що, якщо між з і АС – прямий кут, то він прямій між з і ВС.
Доведемо цю теорему:
- ВА – відрізок, що складає з площиною α кут 90 град.;
- СА – відрізок прямої, що є похилій;
- з – проходить через точку С і має прямий кут з відрізком ВС.
Проводимо КС || ВА. Значить, він становить кут 90 градусів по відношенню до α. Це означає, що він становить кути 90 градусів зі всіма прямими, що знаходяться в α. Між КС і с – кут 90 град., оскільки вона теж належить α.
Будь-які два відрізки, які паралельні один одному, задають площину. Тому існує площину β через відрізки ВА і КС. Пряма з ⊥ СВ і з ⊥ КС, тобто вона становить кут 90 градусів з кожної прямої, що належить β, відрізку СА в тому числі.
Застосування теореми
Ми навели вам доказ теореми про три перпендикулярах і оберненої теореми. Як ви могли переконатися, для доказу нам знадобилися найпростіші і базові аксіоми стереометрії. Сама теорема про три перпендикулярах має дуже широке застосування у вирішенні різних завдань.
Увага! Не існує такої математичної задачі, яка не має аналогій в реальному, повсякденному житті. Коли мова заходить про геометрії, особливо про стереометрії, то це стає помітним ще більше.
Для того щоб показати широту застосування доведеною нами теореми, розглянемо дві цікаві завдання з її застосуванням.
Завдання 1
У трикутник вписано коло. Через центр цього кола Про проведена пряма SO, складова з площиною трикутника кут 90 градусів. Чи вірно твердження, що точка S віддалена від сторін на однакову відстань?
Рішення:
Оскільки радіус кола ОА становить зі стороною трикутника (як радіус і дотична до кола) 90 град., то за теоремою про три перпендикулярах SA становить трикутника зі стороною кут 90 град.
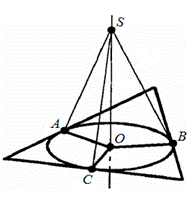
Проаналізуємо SAO. Оскільки SO складає з площиною, в якій розташований трикутник, кут 90 град., то SAO є прямокутним трикутником, до якого можна застосувати теорему Піфагора:
![]() ,
,
де r = АТ = У = — радіус кола.
Розглядаючи СОБ і SOC і застосовуючи до них ті ж самі обчислення, отримуємо їх гіпотенузи:
![]() і
і
![]()
Таким чином, бачимо, що SA=SB=…. Це означає, що так, точка S віддалена від сторін на однакову відстань.
Завдання 2
Є прямокутний трикутник АВС. Висота СН дорівнює 9,6. З кута (90 град.) до площини трикутника проведено відрізок СМ, який утворює перпендикулярність з площиною. Його довжина дорівнює 28. Знайдіть найкоротшу відстань між М і гіпотенузою.
Ознайомимося з рішенням:
СН є висотою, МН можна розглядати як похилу.
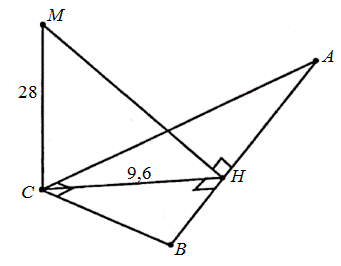
Тоді СН є не тільки висотою трикутника, але і проекцією МН на площину трикутника.
Оскільки між СН і АВ кут 90 град., то по розглянутій вище теоремою МН ⊥ АВ (похила пряма). Таким чином, МН і є найкоротший відрізок між точкою М і АВ.
МСН – прямокутний трикутник, оскільки МС ⊥ СН. А значить, можна застосувати теорему Піфагора:
![]()
Довжина шуканого відрізка знайдено.
Корисне відео: доказ теореми про три перпендикулярах
Корисне відео: завдання на теорему про три перпендикулярах
Висновок
Таким чином, ми дізналися, що таке теорема про три перпендикулярах, навчилися доводити її, побачили, яким чином вона може бути застосована в реальних задачах. Крім того, ми повторили ключові питання планіметрії. Теорема про три перпендикулярах є однією з найважливіших теорем стереометрії, без якої неможливе вирішення майже не однієї задачі.
