Багато технічні, економічні та соціальні питання прогнозуються за допомогою кривих. Найбільш використовуваним типом серед них є парабола, а точніше-її половина. Важливою складовою будь-якої параболічної кривої є її вершина, визначення точних координат якої іноді грає ключову роль не тільки в самому відображенні протікання процесу, але і для наступних висновків. Про те, як знайти її точні координати, і піде мова в даній статті.
Початок пошуку
Перед тим як перейти до пошуку координат вершини параболи, ознайомимося з самим визначенням і його властивостями. У класичному розумінні параболою називається таке розташування точок, які вилучені на однаковій відстані від даної точки (фокус, точка F), а також від прямої, яка не проходить через точку F. Розглянемо дане визначення більш предметно на малюнку 1.
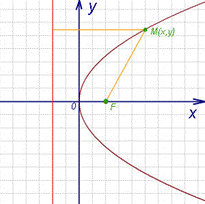
Малюнок 1. Класичний вид параболи
На малюнку зображена класична форма. Фокусом є точка F. Директрисою в даному випадку буде вважатися пряма паралельна осі Y (виділена червоним кольором). З визначення можна впевнитися, що абсолютно будь-яка точка кривої, не рахуючи фокуса, має собі подібну з іншого боку, віддалену на такому ж відстань від осі симетрії, як і сама. Більш того, відстань від будь-якої з точок на параболі дорівнює відстані до директриси. Забігаючи вперед, скажемо, що центр функції не обов’язково повинен знаходитися в початку координат, а гілки можуть бути спрямовані в різні сторони.
Парабола, як і будь-яка інша функція, що має свій запис у вигляді формули:
(1).
У зазначеній формулі буква «s» означає параметр параболи, яка дорівнює відстані від фокуса до директриси. Також є й інша форма запису, зазначено ГМТ, що має вигляд:
(2).
Така формула використовується при вирішенні задач в галузі математичного аналізу і застосовується частіше, ніж традиційна (в силу зручності). Надалі будемо орієнтуватися на другу запис.
Розрахунок коефіцієнтів та основних точок параболи
До числа основних параметрів прийнято відносити розташування вершини на осі абсцис, координати вершини на осі ординат, параметр директриси.
Чисельне значення координати вершини на осі абсцис
Якщо рівняння параболи задано в класичному вигляді (1), то значення абсциси в шуканій точці буде дорівнювати половині значення параметра s (половині відстані між директрисою і фокусом). У випадку, якщо функція представлена у вигляді (2), x нульове розраховується за формулою:
(3).
Тобто, дивлячись на цю формулу, можна стверджувати, що вершина буде знаходитися в правій половині відносно осі y в тому випадку, якщо один з параметрів a або b буде менше нуля.
Рівняння директриси визначається наступним рівнянням:
(4).
Значення вершини на осі ординат
Чисельне значення місцезнаходження вершини для формули (2) на осі ординат можна знайти за такою формулою:
.
Звідси можна зробити висновок, що у разі якщо а<0, то вершина кривої буде знаходитися у верхньої півплощини, в іншому випадку – в нижній. При цьому точки параболи будуть володіти тими ж властивостями, що були згадані раніше.
Якщо дана класична форма запису, то більш раціональним буде обчислення значення розташування вершини на осі абсцис, а через нього і подальше значення ординати. Зазначимо, що для форми запису (2), вісь симетрії параболи, у класичному поданні, буде збігатися з віссю ординат.
Важливо! При вирішенні завдань з використанням рівняння параболи насамперед виділіть основні значення, які вже відомі. Більш того, не зайвим буде, якщо будуть визначені відсутні параметри. Такий підхід заздалегідь дасть більший «простір для маневру» та більш раціональне рішення. На практиці намагайтеся використовувати запис (2). Вона більш проста для сприйняття (не доведеться перевертати координати Декарта), до того ж переважна кількість завдань пристосоване саме під таку форму запису.
Побудова кривої параболічного типу
Використовуючи поширену форму запису, перед тим як побудувати параболу, потрібно знайти її вершину. Простіше кажучи, необхідно виконати наступний алгоритм:
- Знайти координату вершину на осі X.
- Знайти координату розташування вершини на осі Y.
- Підставляючи різні значення залежної змінної X, знайти відповідні значення Y і побудувати криву.
Тобто алгоритм не являє собою нічого складного, основний акцент робиться на тому, як знайти вершину параболи. Подальший процес побудови можна вважати механічним.
За умови, що дано три точки, координати яких відомі, перш за все необхідно скласти рівняння самої параболи, а потім повторити порядок дій, який був описаний раніше. Оскільки в рівнянні (2) присутні 3 коефіцієнта, то, використовуючи координати точок, обчислимо кожне з них:
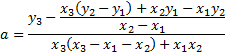(5.1).
(5.2).
(5.3).
У формулах (5.1), (5.2), (5.3) застосовуються відповідно до тих точок, які відомі (наприклад А (
B
(C (
. Таким шляхом знаходимо рівняння параболи по 3 точкам. З практичної сторони такий підхід не є самим «приємним», однак він дає чіткий результат, на основі якого згодом будується сама крива.
При побудові параболи завжди повинна бути присутніми вісь симетрії. Формула осі симетрії для запису (2) буде мати такий вигляд:
(6).
Тобто знайти вісь симетрії, якої симетричні всі точки кривої, не становить праці. Точніше, вона дорівнює першої координати вершини.
Наочні приклади
Приклад 1. Припустимо, маємо рівняння параболи:
Потрібно знайти координати вершини параболи, а також перевірити, чи належить точка D (10; 5) даної кривої.
Рішення: Перш за все перевіримо належність згаданої точки самої кривої
Звідки робимо висновок, що зазначена точка не належить заданої кривої. Знайдемо координати вершини параболи. З формул (4) і (5) отримуємо таку послідовність:
Виходить, що координати на вершині, в точці О, наступні (-1,25; -7,625). Це говорить про те, що наша парабола бере свій початок в 3-й чверті декартової системи координат.
Приклад 2. Знайти вершину параболи, знаючи три точки, які їй належать: A (2;3), B (3;5), C (6;2). Використовуючи формули (5.1), (5.2), (5.3), знайдемо коефіцієнти рівняння параболи. Отримаємо наступне:
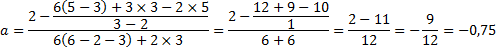
Використовуючи отримані значення, отримаємо наступні рівняння:
На малюнку задана функція буде виглядати наступним чином (малюнок 2):
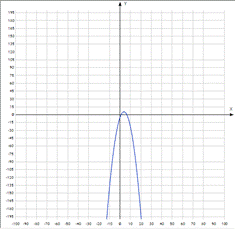
Малюнок 2. Графік параболи, що проходить через 3 точки
Тобто графік параболи, що проходить за трьома заданими точками, буде мати вершину в 1-й чверті. Однак гілки даної кривої спрямовані вниз, тобто є зміщення параболи від початку координат. Така побудова можна було передбачити, звернувши увагу на коефіцієнти a, b, c.
Зокрема, якщо a1 крива буде розтягнута, а якщо менше 1 – стиснута.
Константа c відповідає за «рух» кривий уздовж осі ординат. Якщо c>0, то парабола «повзе вгору, в іншому випадку – вниз. Щодо коефіцієнту b, то визначити ступінь впливу можна лише змінивши форму запису рівняння, привівши її до наступного вигляду:
Якщо коефіцієнт b>0, то координати вершини параболи будуть зміщені вправо на b одиниць, якщо менше – то на b одиниць вліво.
Важливо! Використання прийомів визначення зміщення параболи на координатній площині часом допомагає економити час при вирішенні завдань або дізнатися про можливе перетину параболи з іншого кривий ще до побудови. Зазвичай дивляться тільки на коефіцієнт a, так як саме він дає чітку відповідь на поставлене питання.
Корисне відео: як знайти вершину параболи
Корисне відео: як легко скласти рівняння параболи з графіка
Висновок
Такий як алгебраїчний процес, як визначення вершин параболи, не є складним, але при цьому досить трудомісткий. На практиці намагаються використовувати саме другу форму запису з метою полегшення розуміння графічного рішення і рішення в цілому. Тому настійно рекомендуємо використовувати саме такий підхід, і якщо не пам’ятати формули координати вершини, то хоча б мати шпаргалку.
