З далеких часів і донині пошук ознак рівності фігур вважається базовою задачею, яка є основою основ геометрії; сотні теореми доводяться з використанням ознак рівності. Вміння доводити рівність і подібність фігур — важливе завдання у всіх сферах будівництва.
Застосування навичок на практиці
Припустимо, що у нас є фігура, накреслена на аркуші паперу. При цьому у нас є і транспортир лінійка, за допомогою яких ми можемо заміряти довжини відрізків і кути між ними. Як перенести на другий аркуш паперу фігуру таких же розмірів або збільшити її масштаб у два рази.
Ми знаємо, що трикутник — це фігура, що складається з трьох відрізків, які називаються сторонами, утворюють кути. Таким чином, існує шість параметрів — три сторони і три кути, які визначають цю фігуру.
Однак, вимірявши величину всіх трьох сторін і кутів, перенести дану фігуру на іншу поверхню виявиться непростим завданням. Крім того, є сенс поставити питання: а чи буде знання параметрів двох сторін і одного кута, або всього лише трьох сторін.
Вимірявши довжину двох сторін і кут між ними, потім відкладемо цей кут на новому листку паперу, так ми зможемо повністю відтворити трикутник. Давайте розберемося, як це зробити, навчимося доводити ознаки, за якими їх можна вважати однаковими, і визначимося з тим, яке мінімальне число параметрів достатньо знати, щоб отримати впевненість у тому, що однакові трикутники.
Важливо ! Фігури називаються однаковими, якщо відрізки, що утворюють їх сторони і кути рівні між собою. Подібними називаються ті фігури, у яких сторони і кути пропорційні. Таким чином, рівність — це подібність з коефіцієнтом пропорційності 1.
Які існують ознаки рівності трикутників, дамо їх визначення:
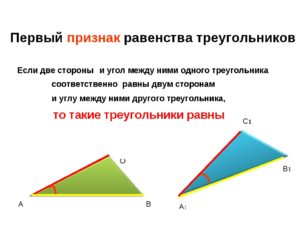
- перша ознака рівності: два трикутника можна вважати однаковими, якщо рівні дві сторони, а також кут між ними.
- друга ознака рівності трикутників: два трикутники будуть однаковими, якщо однакові два кута, а також відповідна сторона між ними.
- третя ознака рівності трикутників: трикутники можна вважати однаковими, коли всі їх сторони мають однакову довжину.
Як довести, що трикутники рівні. Наведемо доказ рівності трикутників.
Доказ 1 ознаки
Довгий час серед перших математиків даний ознака вважався аксіомою, однак, як виявилося, його можна геометрично довести, спираючись на базові аксіоми.
Розглянемо два трикутника — KMN і K1M1N1. Сторона КМ має таку ж довжину, як і K1M1, а KN = K1N1. А кут MKN дорівнює кутах KMN і M1K1N1.
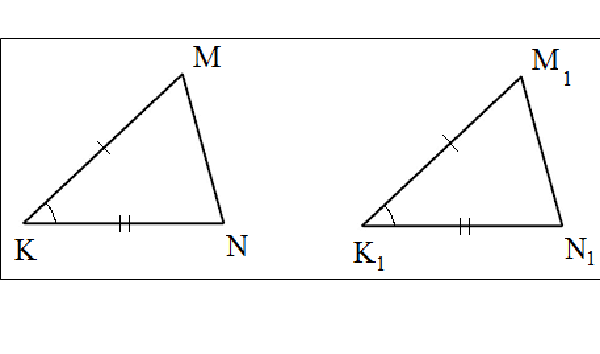
Якщо розглядати KM та K1M1, KN і K1N1 як два промені, які виходять з однієї точки, то можна сказати, що між цими парами променів однакові кути (це задано умовою теореми). Здійснимо паралельний перенос променів K1M1 і K1N1 з точки K1 в точку К. Внаслідок цього перенесення промені K1M1 і K1N1 повністю співпадуть. Відкладемо на промені K1M1 відрізок довжиною КМ, що бере свій початок в точці К. Оскільки за умовою отриманий відрізок і буде дорівнює відрізку K1M1 точки М і M1 збігаються. Аналогічно і з відрізками KN і K1N1. Таким чином, переносячи K1M1N1 так, що точки K1 і До збігаються, а дві сторони накладаються, отримуємо повний збіг і самих фігур.
Важливо! В інтернеті зустрічаються докази рівності трикутників по двох сторонах і куту за допомогою алгебраїчних та тригонометричних тотожностей з чисельними значеннями сторін і кутів. Проте історично і математично ця теорема була сформульована задовго до алгебри і раніше, ніж тригонометрії. Для доказу цієї ознаки теореми використовувати що-небудь, крім базових аксіом, некоректно.
Доказ 2 ознаки
Доведемо друга ознака рівності по двом кутам і стороні, грунтуючись на першому.
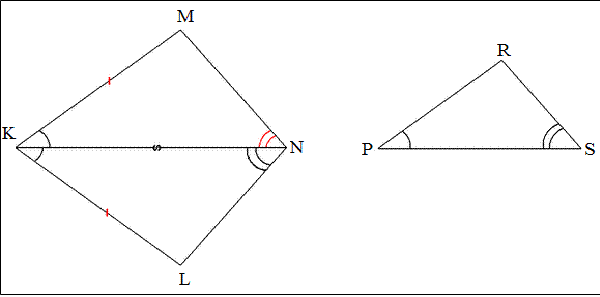
Доказ 2 ознаки
Розглянемо KMN і PRS. До дорівнює Р, N дорівнює S. Сторона КN має таку ж довжину, як і РЅ. Необхідно довести, що KMN і PRS — однакові.
Відобразимо точку М відносно променя КN. Отриману точку назвемо L. При цьому довжина сторони, КМ = КL. NKL дорівнює PRS. KNL дорівнює RSP.
Оскільки сума кутів дорівнює 180 градусів, то KLN дорівнює PRS, а значить PRS і KLN – однакові (подібні) по обох сторонах і куті, згідно з першою ознакою.
Але, так як KNL дорівнює KMN, то KMN і PRS — дві однакові фігури.
Доказ 3 ознаки
Як встановити, що трикутники рівні. Це прямо випливає з доведення другої ознаки.
Довжина KN = PS. Оскільки ДО = Р, N = S, KL=KM, при цьому КN = KS, MN=ML, то:
Це означає, що обидві фігури є подібними один до одного. Але так як їх сторони однакові, то і вони також рівні.
Ознаки рівності та подібності випливає безліч наслідків. Одне з них полягає в тому, що для того, щоб визначити, чи дорівнюють два трикутника або немає, необхідно знати їх властивості, однакові:
- всі три сторони;
- обидві сторони і кут між ними;
- обидва кута і сторона між ними.
Використання ознаки рівності трикутників для вирішення завдань
Наслідки першої ознаки
У ході докази можна прийти до ряду цікавих і корисних наслідків.
- Паралелограм. Той факт, що точка перетину діагоналей паралелограма ділить їх на дві однакові частини — наслідок ознак рівності і цілком піддається доведенню.Сторони додаткового трикутника (при дзеркальному побудові, як в доказах, які ми виконували) — паралельні сторонам головного (сторони паралелограма).
- Якщо є два прямокутних трикутника, у яких однакові гострі кути, то вони подібні. Якщо при цьому катет першого дорівнює катету другого, то вони рівні. Зрозуміти це досить легко — в усіх прямокутних трикутників є прямий кут. Тому ознаки рівності для них більш прості.
- Два трикутника з прямими кутами, у яких два катета мають однакову довжину, можна вважати однаковими. Це пов’язано з тим, що між двома катетами кут завжди дорівнює 90 градусів. Тому за першою ознакою (по двох сторонах і куту між ними) всі трикутники з прямими кутами і однаковими катетами — рівні.
- Якщо є два прямокутних трикутника, і у них один катет і гіпотенуза рівні, значить і однакові трикутники.
Доведемо цю просту теорему.
Є два прямокутних трикутника. У однієї сторони a, b, c, де с — гіпотенуза; a, b — катети. У другого боку n, m, l, де l — гіпотенуза; m, n — катети.
По теоремі Піфагора один з катетів дорівнює:
;
.
Таким чином, якщо n = a, l = з (рівність катетів і гипотенуз), відповідно і другі катети дорівнюють. Фігури, відповідно, будуть рівні по третьому ознакою (за трьома сторонами).
Відзначимо ще один важливий наслідок. Якщо є два рівних трикутника, і вони подібні з коефіцієнтом подібності k, тобто попарні відносини всіх їхніх сторін дорівнюють k, то ставлення їх площ одно k2 .
Перша ознака рівності трикутників. Відеоурок з геометрії 7 клас
Геометрія 7 Перша ознака рівності трикутників
Висновок
Розглянута нами тема допоможе кожному учневі краще розібратися в базових геометричних поняттях і підвищити свої навички у найцікавіший світ математики.
