В сучасному машинобудуванні використовується маса елементів і запчастин, які мають у своїй структурі як зовнішні кола, так і внутрішні. Самим яскравим прикладом можуть служити корпус підшипника, деталі моторів, вузли маточини і багато іншого. При їх виготовленні застосовуються не тільки високотехнологічні пристрої, але і знання з геометрії, зокрема інформація про окружностях трикутника. Більш детально з подібним знаннями познайомимося нижче.
Яка вписана окружність, а яка описана
Перш за все згадаємо, що окружністю називається нескінченну безліч точок, віддалених на однаковій відстані від центру. Якщо всередині многокутника допускається побудувати окружність, яка з кожною стороною буде мати тільки одну спільну точку перетину, то вона буде називатися вписаною. Описаної окружністю (не коло, це різні поняття) називається таке геометричне місце точок, при якому у побудованої фігури з заданим гратки загальними точками будуть тільки вершини многокутника. Ознайомимося з цими двома поняттями на більш наочному прикладі (див. рис 1.).
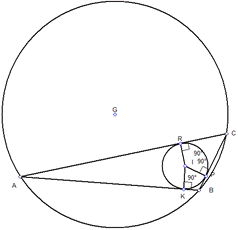
Малюнок 1. Вписана і описана кола трикутника
На зображенні побудовані дві постаті великого і малого діаметрів, центри яких знаходяться G і I. Коло більшого значення називається описаною дкр-ма Δ ABC, а малого – навпаки, вписаної в Δ ABC.
Для того щоб описати навколо трикутника дкр-ть, потрібно провести через середину кожної сторони перпендикулярну пряму (тобто під кутом 90°) – це точка перетину, вона відіграє ключову роль. Саме вона буде представляти собою центр описаного кола. Перед тим як знайти окружність, її центр у трикутник, потрібно побудувати для кожного кута биссектрису, після чого виділити точку перетину прямих. Вона в свою чергу буде центром вписаного дкр-ти, а її радіус при будь-яких умовах буде перпендикулярний будь-якої із сторін.
На питання:«Яка кількість вписаних кіл може бути для багатокутника з трьома кутами?» відповімо відразу, що в будь-який трикутник можна вписати коло і притому тільки одну. Тому що існує лише одна точка перетину всіх бісектрис і одна точка перетину перпендикулярів, що виходять з середин сторін.
