З метою підвищення точності розв’язання практичних завдань, як в будівництві, так і економіці іноді потрібен більш потужний інструмент, який давав би відповідь на нестандартні умови. Наприклад, обчислення площі покриття не традиційної форми (половини параболи), виготовлення конструкцій, що вилучається або забудовуючи площа і багато іншого. Таким інструментом є саме інтеграл, рамки обчислення якого задає сам користувач. Наведемо приклади обчислення визначеного інтеграла з доказом його властивостей,
Значення поняття
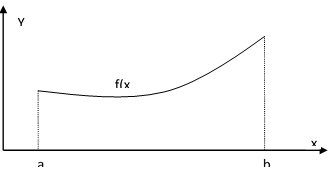
Малюнок 1. Загальний вигляд криволінійної трапеції.
Незважаючи на теоретичне обгрунтування, відразу дамо більш чітке поняття цього терміна. Визначеним інтегралом вважається площа криволінійної трапеції, яка за підстави приймає знизу – вісь абсцис, а знизу саму функцію. Більш наочно це зображено на рисунку 1. Таке трактування називається геометричним, і більш зрозуміло, ніж інші.
В більш класичному визначенні, чисельне вираження інтеграла є величина якоїсь первісної на вибраному і обмеженому проміжку (відрізку). На практиці значення такого приросту може бути як більше, так і менше нуля. Щодо значення площі дане питання залежить від того, в якій півплощини знаходиться крива (верхній або нижній), такий і буде знак (на практиці його значення відкидають). У чисельному вираз наше визначення має таку формулу:
![]()
Спираючись на вищезгадану формулу можемо стверджувати, що визначений інтеграл являє собою різницю первісної в крайніх точках обраного інтервалу (такий підхід до визначення називають формула Ньютона – Лейбніца).
